视差 Cubmap

2016-9-7

注：本文所介绍的技术来自于 https://seblagarde.wordpress.com/2012/09/29/image-based-lighting-approaches-and-parallax-corrected-cubemap/ 这篇文章中的 Parallax correction for local cubemaps 章节。

使用 Cubmap 可以模拟出环境的反射，预先将环境渲染到 Cubmap 中，从而避免在游戏运行时对环境的实时反射产生的消耗，而且这样做表现效果也非常好。在一些户外环境尤其适用，比如说车身反射外部的环境。但是在一些室内的环境中，普通的 Cubmap 反射通常会产生奇怪的效果。

Demo1	天下手游截图1	天下手游截图2

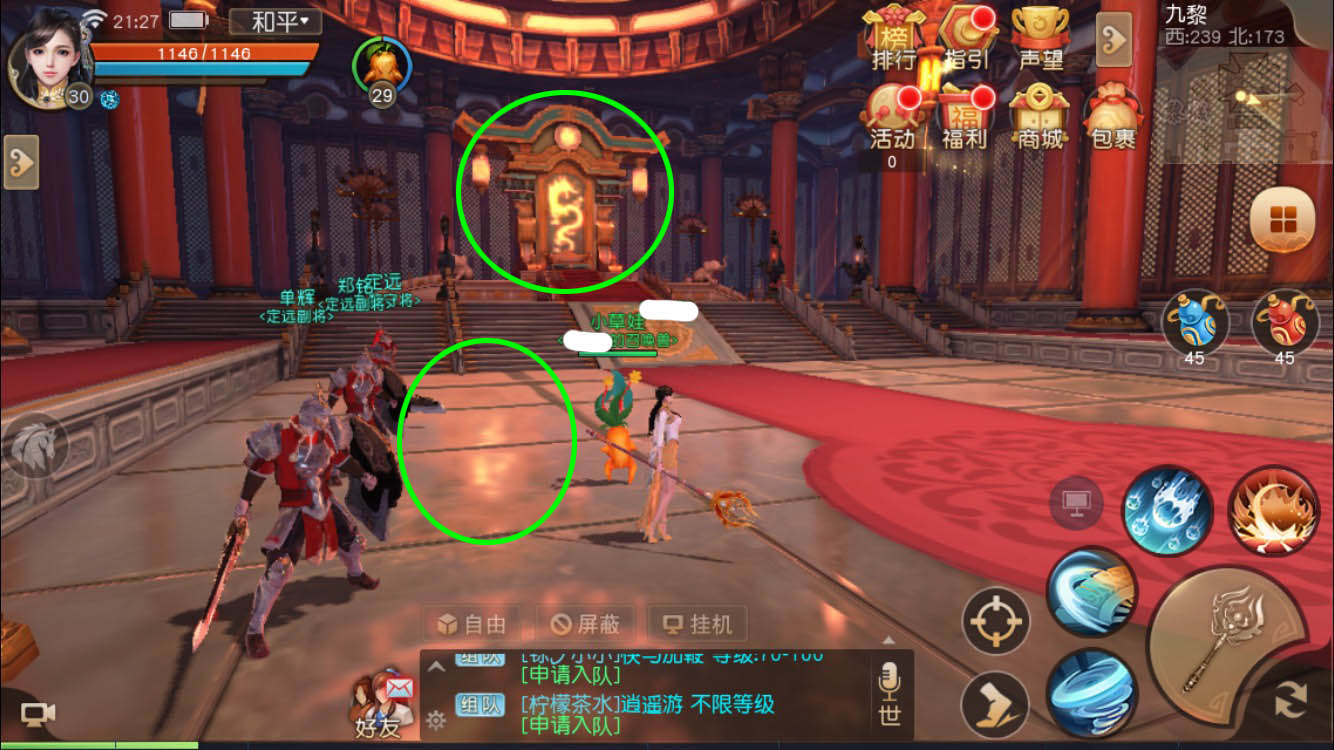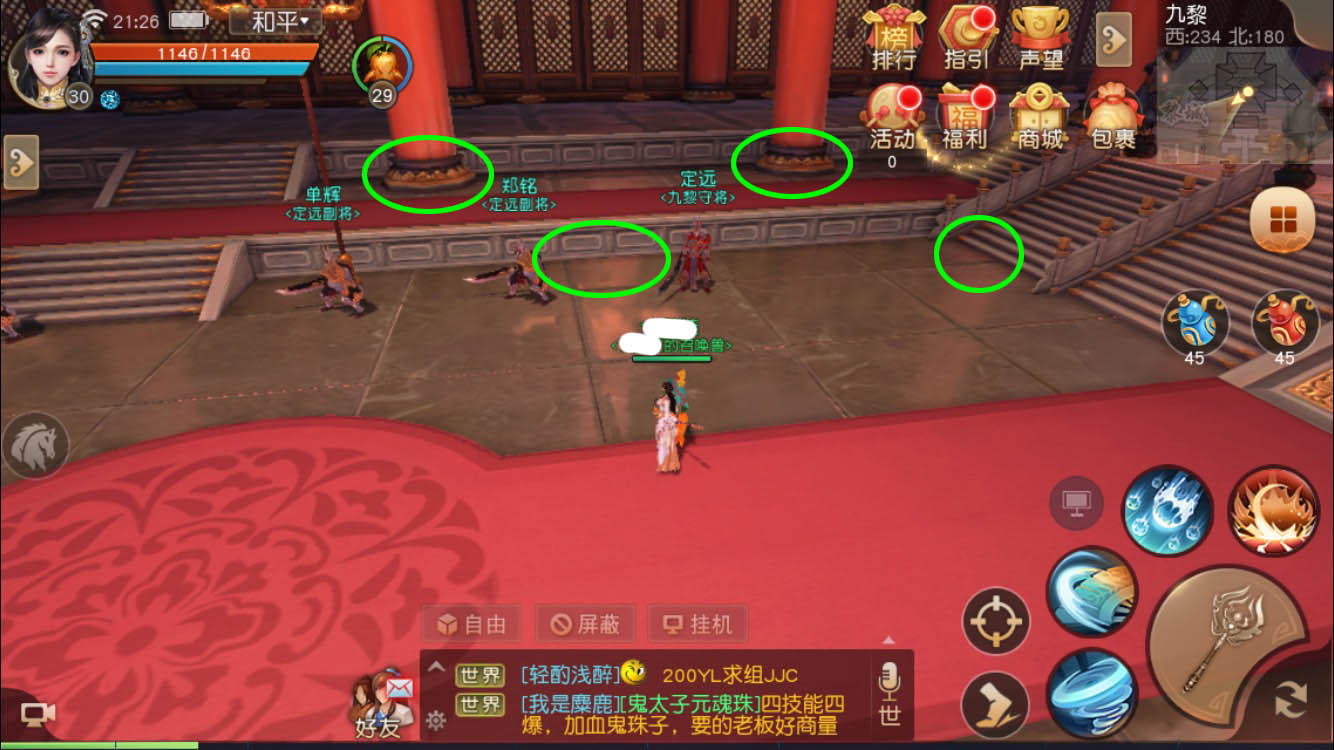
Demo1 中，可以看到大理石地面的反射错了。 天下手游截图1 中，柱子的反射错位了。 天下手游截图2 中，王座的反射明显和模型产生了错位，不是正常的角度。这是普通计算 Cubmap 的反射射线方式所无法避免的

// 通过视线向量和法线向量计算反射向量
float3 reflDir = reflect(viewDir, normal);
// 使用反射向量采样 Cubmap
fixed4 col = texCUBE(_EnvMap, reflDir);

一般我们认为 Cubmap 是一个无穷大的立方体包围着要产生反射的物体，上面的效果和这个假设是匹配的。下面我们使用一种新的方法来计算反射向量。

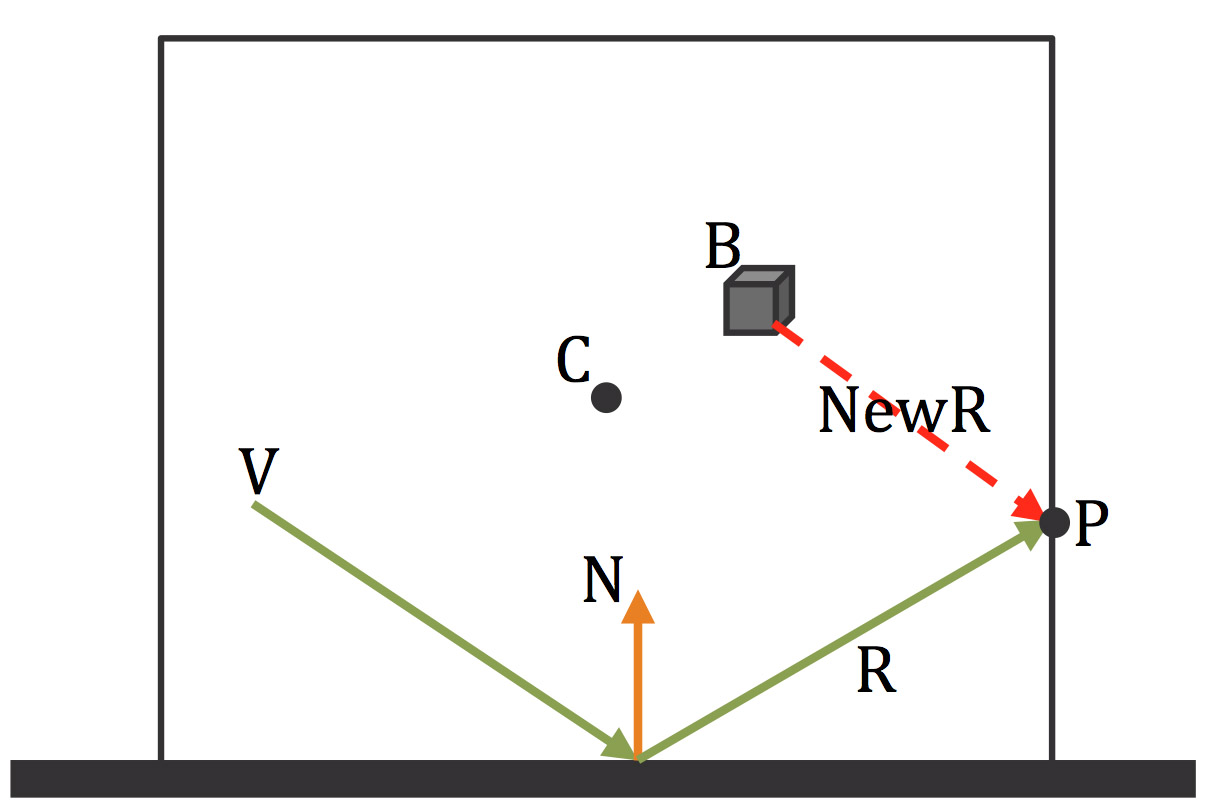
在 Parallax Collection for Local Cubmaps 中提到点B和点C可以是不重叠的两个点，我在制作中发现如果要得到比较好的效果，B和C两点多为重叠的情况，当然B和C两点也可以使用一个偏移量来达到微调的作用。

图中，R 是使用上文中介绍的方法计算得到的反射向量，R 射线和假想的 Cubmap 范围盒交点于 P，再从产生 Cubmap 快照的点 B 到 P 形成的新的向量即是新的反射向量 NewR。这些步骤中最为关键的就是求出交点 P。

求交点 P 实际上就是在求射线和平面的交点。公式的推导请查看这里，本文就直接拿来使用了：

\[ t = { (P_{o} - R_{o}) \cdot P_{N} \over R_{D} \cdot P_{N} } \]

当公式中的分母为 0 的时候，就是射线和平面没有交点的情况，我并不清楚当一个数被 0 除时着色器在不同设备上会发生什么，一般来说这种情况在常规的观察角度时极少发生，即使发生了也只会影响到一个像素，我在测试中没有发现过因此带来的副作用，所以暂时就忽略了。

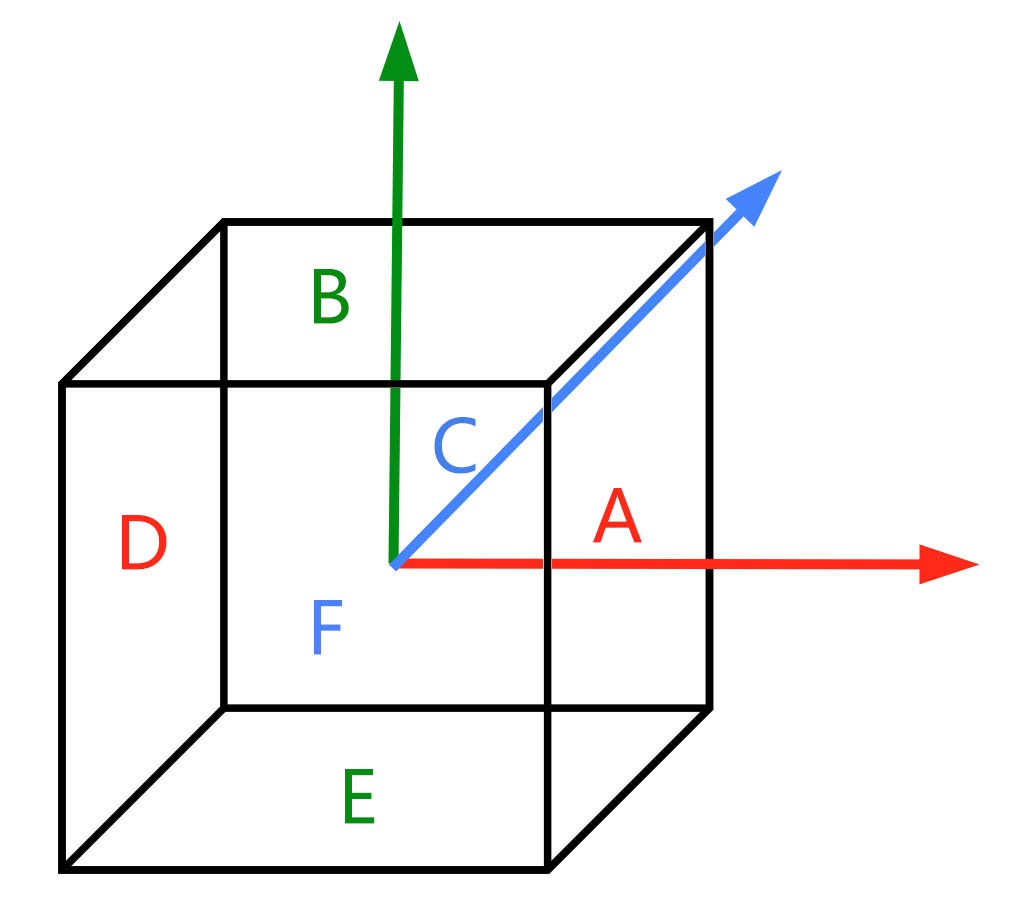
先说明下以后的计算所基于的一个前提，就是假想的 Cubmap 范围盒（上图中外层的黑色细线矩形）是一个 AABB。AABB 的全称是 Axis Aligned Bounding Box，从字面上翻译为轴对齐的包围盒，最重要的一点是轴对齐的，也就是说这个包围盒的任何一条边和 XYZ 三根正交轴不是平行就是垂直。我们知道 Cubmap 有六个面，如果这六个面是任意的，那么将会增加很多射线和平面检测的计算量，但是由于有了 AABB，这一部分的计算量被大大减少了。

面向三根基轴正方向的三个面（ABC）和射线的交点可以一起计算，而另外三个面（DEF）一起计算。这是由于面 A 的 $$$ P_{N} = (1,0,0) $$$，面 B 的 $$$ P_{N} = (0,1,0) $$$，面 C 的 $$$ P_{N} = (0,0,1) $$$，其它三个面同理。同样公式中的 $$$ P_{o} $$$ 也是类似的。这就是为什么 ABC 这三个面可以同时计算交点了。下面给出着色器代码：

float3 viewDir = IN.worldPos - _WorldSpaceCameraPos;
float3 worldNormal = IN.worldNormal;
float3 reflectDir = reflect (viewDir, worldNormal);
// 得到反射向量
reflectDir = normalize(reflectDir);

// _BoxPosition 表示假想的 Cubmap 范围盒的中心点
// _BoxSize 表示假想的 Cubmap 范围盒的尺寸
half3 boxStart = _BoxPosition - _BoxSize * 0.5;
half3 firstPlaneIntersect = (boxStart + _BoxSize - IN.worldPos) / reflectDir;
half3 secondPlaneIntersect = (boxStart - IN.worldPos) / reflectDir;
// 上面得到了六个 t，通过比较这六个 t 的大小，从而得到交点 P 处的 t 值
half3 furthestPlane = max(firstPlaneIntersect, secondPlaneIntersect);
half3 intersectDistance = min(min(furthestPlane.x, furthestPlane.y), furthestPlane.z);
// 计算交点 P 的坐标
half3 intersectPosition = IN.worldPos + reflectDir * intersectDistance;
// 使用新的反射向量采样 Cubmap
fixed4 reflcol = texCUBElod(_CubeMap, float4(intersectPosition - _BoxPosition, _Roughness));

Demo2	Demo3

Demo2 修正了 Demo1 中的错误

Demo3 添加了扰动法线，并结合纹理的 Mipmap 做出了 Roughness 效果

上文说了，这种计算能够成立的前提是 AABB，但是如果是非 AABB 该怎么办呢，其实很简单就是将值转换到 AABB 中再进行计算。下面就直接给出着色器代码了。

float3 wpos = float3(_Object2World[0].w, _Object2World[1].w, _Object2World[2].w);
float3 viewDir = IN.worldPos - wpos - (_WorldSpaceCameraPos - wpos);
float3 worldNorm = IN.worldNormal;
float3 reflectDir = reflect (viewDir, worldNorm);
reflectDir = normalize(reflectDir);

float3 RayLS = normalize(mul(reflectDir, (float3x3)_Object2World));
float3 PositionLS = mul((float3x3)_World2Object, IN.worldPos - wpos);
float3 Unitary = _BoxSize;
float3 FirstPlaneIntersect = (Unitary - PositionLS) / RayLS;
float3 SecondPlaneIntersect = (-Unitary - PositionLS) / RayLS;
float3 FurthestPlane = max(FirstPlaneIntersect, SecondPlaneIntersect);
float Distance = min(FurthestPlane.x, min(FurthestPlane.y, FurthestPlane.z));
float3 IntersectPositionWS = PositionLS + RayLS * Distance;
float3 ReflDirectionWS = IntersectPositionWS - _BoxPosition;
fixed4 reflcol = texCUBElod(_CubeMap, float4(float3(ReflDirectionWS.x,ReflDirectionWS.y,-ReflDirectionWS.z), _Roughness));

使用这种方法我们还可以实现很多有趣的效果，比如像下面这样的：

Demo4	Demo5

左图中窗户内部的物体是实实在在的模型，而右图中窗户内部的看似是有物体的，但其实是通过上文介绍的方法进行的模拟，效果非常好，减少了大量房屋内部的模型消耗。同时窗外的景色也因为 Cubmap 而没有丢失。

放上 Overwatch 的截图，应该也是使用的这个技术吧。最后感谢 Simon 的文章，让我了解到了更多这方面的知识。