反射 折射

2017-11-24

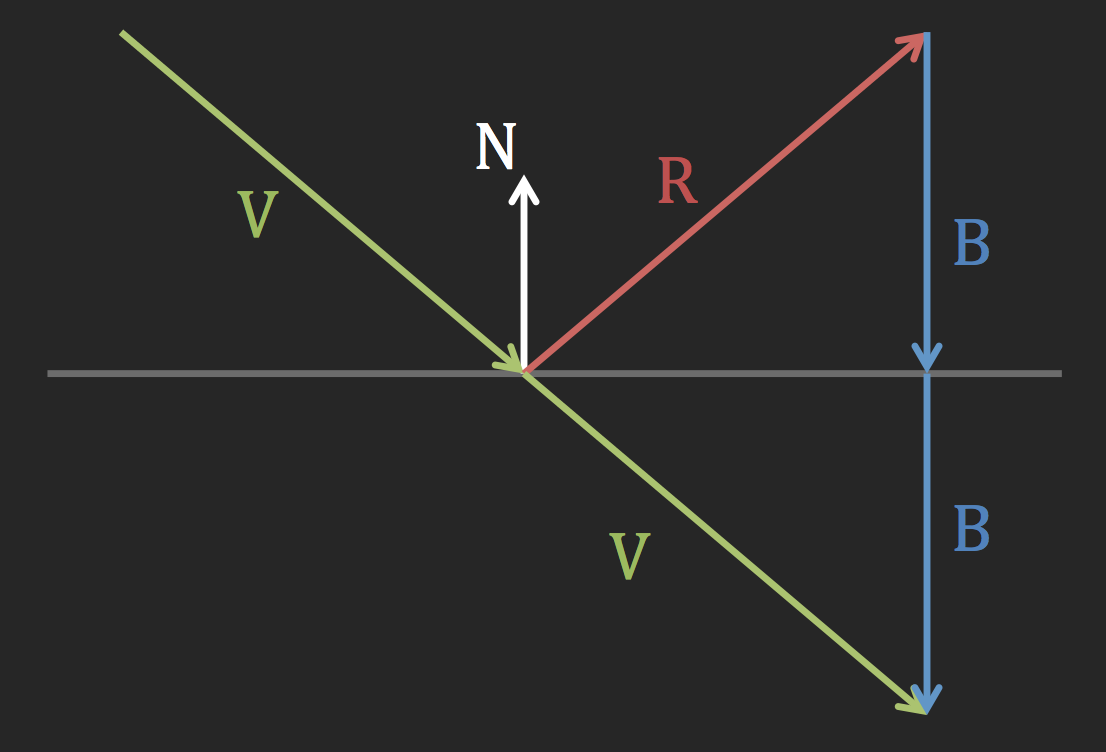
反射

public static Vector3 Reflect(Vector3 v, Vector3 n)
{
    Vector3 b = Vector3.Dot(v, n) * n;
    Vector3 r = v - 2 * b;
    return r;
}

计算反射射线的代码配合上图很容易看出来。

折射

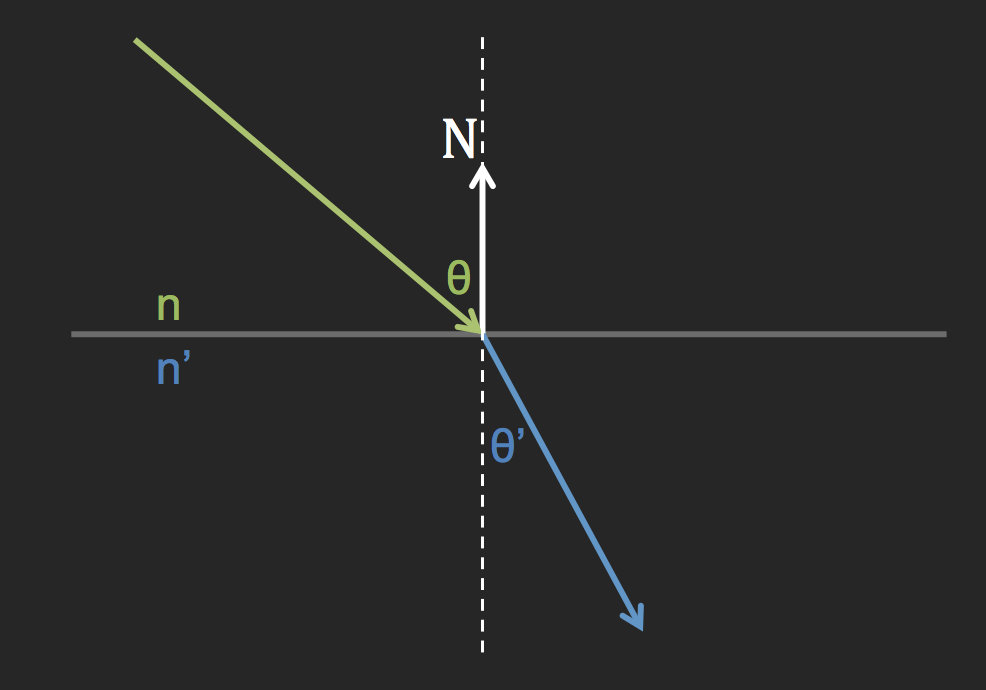
Snell 定律

\[ n \ sin\theta = n' \ sin\theta' \]

折射中有一种称为全反射的现象，这种现象只有当光从光密介质到光疏介质时才会发生，也就是当 \( \theta'\) 大于 90 度时，折射光会消失，变成相对于法线的反射光。

public static bool Refract(Vector3 v, Vector3 n, float ni_over_nt, out Vector3 refracted)
{
    Vector3 uv = v.normalized;
    float dt = Vector3.Dot(uv, n);
    float discriminant = 1.0f - ni_over_nt * ni_over_nt * (1 - dt * dt);
    if(discriminant > 0)
    {
        refracted = ni_over_nt * (uv - n * dt) - n * Mathf.Sqrt(discriminant);
        return true;
    }
    else
    {
        refracted = Vector3.zero;
        return false;
    }
}

计算折射射线的代码可以这样来理解：首先判断是否会出现全反射，根据上文中的描述 \( \theta' \) 大于 90 度就表示出现了全反射，换一种说法就是 \( cos\theta'\) 小于 0。下面就可以从 Snell 定律来计算出 \( cos\theta' \) 的值。

\[ \left\{ \begin{align} & n \ sin\theta = n' \ sin\theta' \tag{EQ1} \\ & sin^2\theta' + cos^2\theta' = 1 \tag{EQ2} \end{align} \right. \]

\[ \left\{ \begin{align} & \because EQ1 \\ n^2 \ sin^2\theta &= n'^2 \ sin^2\theta' \\ sin^2\theta' &= sin^2\theta \ \left( n \over n' \right)^2 \tag{EQ3} \end{align} \right. \]

\[ \left\{ \begin{align} & \because EQ2 \\ cos^2\theta' &= 1 - sin^2\theta' \tag{EQ4} \end{align} \right. \]

\[ \left\{ \begin{align} EQ3 & \rightarrow EQ4 \\ cos^2\theta' &= 1 - sin^2\theta \ \left( n \over n' \right)^2 \\ cos^2\theta' &= 1 - \left( 1 - cos^2\theta \right) \ \left( n \over n' \right)^2 \tag{EQ5} \end{align} \right. \]

至此，也就得到了 \( cos\theta \) 的值，代码中 discriminant 值的计算方式也由 \( EQ5 \) 得到了验证。

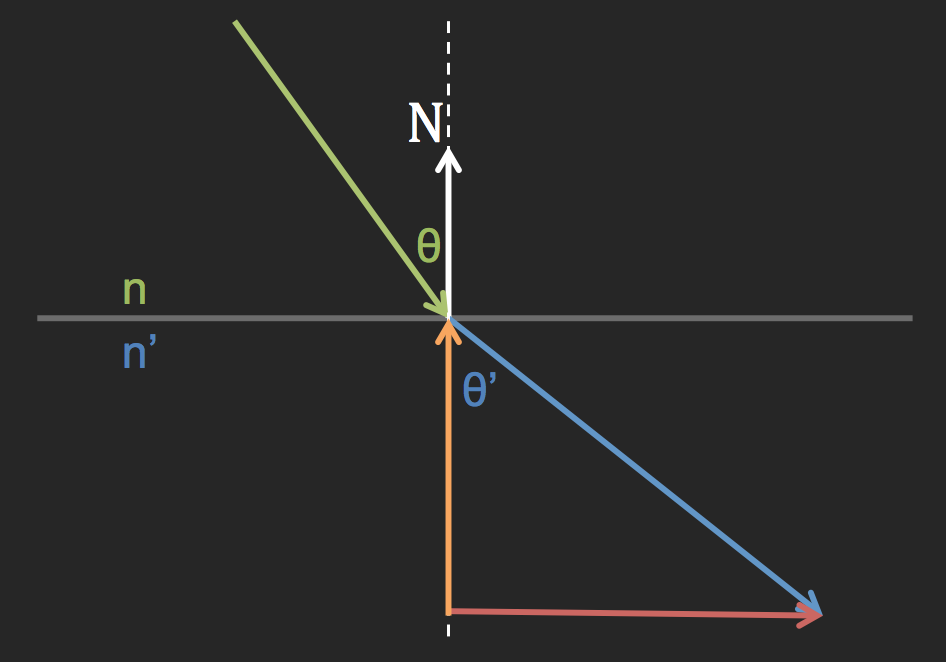
最后当判断完不会出现全反射时，便可计算折射向量了。

refracted = ni_over_nt * (uv - n * dt) - n * Mathf.Sqrt(discriminant); 

将红色向量减去橘黄色向量便得到了折射射线的方向。